参考文章:
1. 均匀分布
torch.nn.init.uniform_(tensor, a=0, b=1)
服从~U(a,b)
2. 正太分布
torch.nn.init.normal_(tensor, mean=0, std=1)
服从~N(mean,std)
3. 初始化为常数
torch.nn.init.constant_(tensor, val)
初始化整个矩阵为常数val
4. Xavier
基本思想是通过网络层时, 输入和输出的方差相同 ,包括前向传播和后向传播。具体看以下博文:
- 为什么需要Xavier 初始化?
文章第一段通过sigmoid激活函数讲述了为何初始化?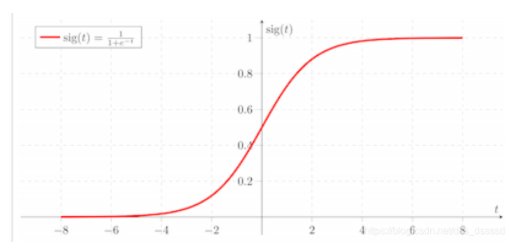
简答的说就是:
- 如果初始化值很小,那么随着层数的传递,方差就会趋于0,此时输入值 也变得越来越小,在sigmoid上就是在0附近,接近于线性, 失去了非线性
- 如果初始值很大,那么随着层数的传递,方差会迅速增加,此时输入值变得很大,而sigmoid在大输入值写倒数趋近于0,反向传播时会遇到 梯度消失 的问题
其他的激活函数同样存在相同的问题。
https://prateekvjoshi.com/2016/03/29/understanding-xavier-initialization-in-deep-neural-networks/
所以论文提出,在每一层网络保证输入和输出的方差相同。
对于Xavier初始化方式,pytorch提供了uniform和normal两种:
torch.nn.init.xavier_uniform_(tensor, gain=1)均匀分布 ~U(−a,a)
其中, a的计算公式: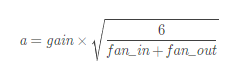
torch.nn.init.xavier_normal_(tensor, gain=1)正态分布~ N(0,std)
其中std的计算公式: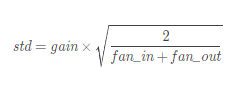
5. kaiming (He initialization)
Xavier在tanh中表现的很好,但在Relu激活函数中表现的很差,所何凯明提出了针对于Relu的初始化方法。
Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification He, K. et al. (2015)
该方法基于He initialization,其简单的思想是:
在ReLU网络中 ,假定每一层有一半的神经元被激活,另一半为0,所以,要保持方差不变,只需要在 Xavier 的基础上再除以2
也就是说在方差推到过程中 ,式子左侧除以2.
pytorch也提供了两个版本:
torch.nn.init.kaiminguniform(tensor, a=0, mode=’fan_in’, nonlinearity=’leaky_relu’), 均匀分布 ~U(−bound,bound)
其中,bound的计算公式: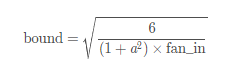
torch.nn.init.kaimingnormal(tensor, a=0, mode=’fan_in’, nonlinearity=’leaky_relu’), 正态分布~N(0,std)
其中,std的计算公式: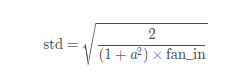
两函数的参数:
a:该层后面一层的激活函数中负的斜率(默认为ReLU,此时a=0)mode:‘fan_in’ (default) 或者 ‘fan_out’. 使用fan_in保持weights的方差在前向传播中不变;使用fan_out保持weights的方差在反向传播中不变
针对于Relu的激活函数 ,基本使用He initialization,pytorch也是使用kaiming 初始化卷积层参数的